高考数学(文科)小题狂做· 基础篇
P87
Q4
若直线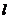 过点
过点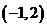 且与直线
且与直线 垂直,则
垂直,则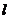 的方程是 ( )
的方程是 ( )
A.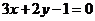
B.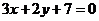
C.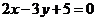
D.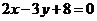
考点说明:直线的方程
问题解答:与题中所给直线垂直的直线的一般式方程可设为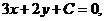 代入点坐标即可;
代入点坐标即可;
对于类似的直线的垂直问题一般有两种解决方法,一种是通过斜率之积为-1先求斜率,然后写出点斜式方程;另一种是通过方向向量设一般式方程,代入点求待定系数即可。
一般地,对于用一般式方程写成的直线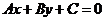 ,其方向向量为
,其方向向量为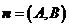 。
。
Q7
若直线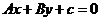 过一、二、三象限,则 ( )
过一、二、三象限,则 ( )
A.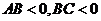
B.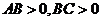
C.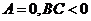
D.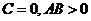
考点说明:直线的方程
问题解答:此类题目建议把方程化为斜截式,比较斜率和纵截距易得答案。
Q8
已知点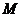 是直线
是直线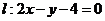 与
与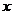 轴的交点,将直线
轴的交点,将直线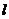 绕点
绕点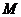 按逆时针方向旋转
按逆时针方向旋转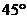 ,得到的直线方程是 ( )
,得到的直线方程是 ( )
A.
B.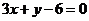
C.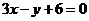
D.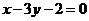
考点说明:直线的方程
问题解答:本题的关键是求出旋转之后的直线的斜率,一般的解决方法是根据原直线的斜率 去求;设旋转之后的直线的倾斜角为
去求;设旋转之后的直线的倾斜角为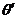 ,依题可知
,依题可知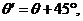 根据两角和的正切公式可得旋转后直线的斜率,再根据点
根据两角和的正切公式可得旋转后直线的斜率,再根据点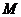 的坐标可求得最终的方程。
的坐标可求得最终的方程。
P88 Q11
两平行直线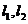 分别过点
分别过点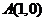 与
与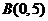 ,则
,则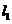 与
与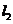 的最大距离为 ( )
的最大距离为 ( )
A.3
B.4
C.5
D.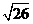
考点说明:平行直线间的距离
问题解答:原本平行直线间的距离应使用两直线的方程来求,实际上,本题中给出的两个点间的距离就是两平行直线间的最大距离,即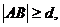 可以通过画图来理解这一结论。
可以通过画图来理解这一结论。
Q12
若过点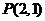 的直线与两坐标轴围成的三角形的面积为4,则这样的直线共有 ( )
的直线与两坐标轴围成的三角形的面积为4,则这样的直线共有 ( )
A.1条
B.2条
C.3条
D.4条
考点说明:直线的方程
问题解答:本题仍然有两种解决方法,一种是根据定点设点斜式方程,然后根据方程求出与坐标轴的交点,再根据三角形面积求解具体值;另一种是根据截距设截距式方程,带入定点后再根据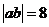 求解具体值。
求解具体值。
Q14
若直线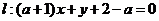 在两坐标轴上的截距相等,则实数
在两坐标轴上的截距相等,则实数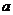 的值为________.
的值为________.
考点说明:直线的方程
问题解答:注意以下结论:若直线在两坐标轴上的截距相等,则直线过原点或斜率为-1,可得本题答案。
Q15
经过点 作直线
作直线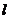 ,若直线
,若直线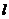 与连结
与连结 的线段总有公共点,则直线
的线段总有公共点,则直线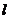 的斜率
的斜率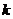 的取值范围为________.
的取值范围为________.
考点说明:直线的斜率
问题解答:本题建议画图解决,求出定点与线段两端点的对应斜率后,注意直线倾斜角的走向(范围,如有没有经过直角)确定斜率是在端点斜率之间还是在端点斜率之外。
Q16
已知直线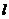 经过直线
经过直线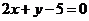 与
与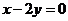 的交点,若点
的交点,若点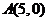 到
到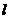 的距离为3,则
的距离为3,则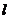 的方程为________.
的方程为________.
考点说明:直线的方程
问题解答:先联立两直线方程求出所过定点,然后设出点斜式,根据点到直线距离公式求解斜率即可
注意:1.利用点斜式求解时注意是否存在斜率不存在的符合要求的直线;
2.实际上可以通过求出的定点与 间的距离与3的关系判断满足条件的解有几个。
间的距离与3的关系判断满足条件的解有几个。

微信小程序
微信扫一扫体验

微信公众账号
微信扫一扫加关注
评论 返回
顶部

发表评论 取消回复